统计学习方法笔记:3.k近邻法
这是我参加mlhub123组织的书籍共读计划的读书笔记,活动见mlhub第一期读书计划
- 阅读章节:第三章:k近邻法
- 开始时间:2018-09-29
- 结束时间:2018-10-23(比较忙)
- 目标:读完第三章,掌握基本概念,产出一篇笔记
- 博客地址
k近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法,本书只讨论分类形式:
- k近邻算法
- k近邻模型
- k近邻法的实现:kd树
k近邻算法
什么是k近邻算法?
给定一个训练集:$T = {(x_1,y_1),(x_2,y_2),…,(x_n,y_n)}$,其中$x_i$为实例的特征向量,$y_i\in \gamma =\{c_1,c_2,…,c_k\}$,输入实例特征向量$x$,输出该实例特征向量的类别$y$
关键点在于是如何进行类别的判断,描述如下:

思想很简单,就是给定一个训练集,输入一个实例,就在训练集中找出与该实例最邻近的k个实例,然后进行多数表决,这k个实例的多数属于某个类,就把该输入实例分为这个类
上面3.1的公式这里解释一下:随着变量j的递增,$c_j$代表不同的类别,每次$x_i$对应的$y_i$会和$c_j$进行比较,如果$y_i$等于$c_j$,该类别计数加一,直到$y_1,y_2,,,y_i$与$c_j$比较完毕,累加之和最高的$c_j$就是输出$y$(意思就是判断输入实例邻域的实例在此类别占据多少个数目),至此,分类成功
k近邻模型
k近邻法使用的模型实际上对应于对特征空间的划分,模型由三个基本要素——距离 度量、k值的选择和分类决策规则决定
模型
通过上面的叙述,当我们知道:
- 训练集
- 距离度量(明可夫斯基距离)
- k值
- 分类决策规则(多数表决)
此时对于任何一个新的输入实例,都可以确定其所属的类
什么是单元?
特征空间中,对每个训练实例点$i_x$,距离该点比其他点更近的所有点组成一个区域,叫作单元(cell),最终会将特征空间划分为下图所示:
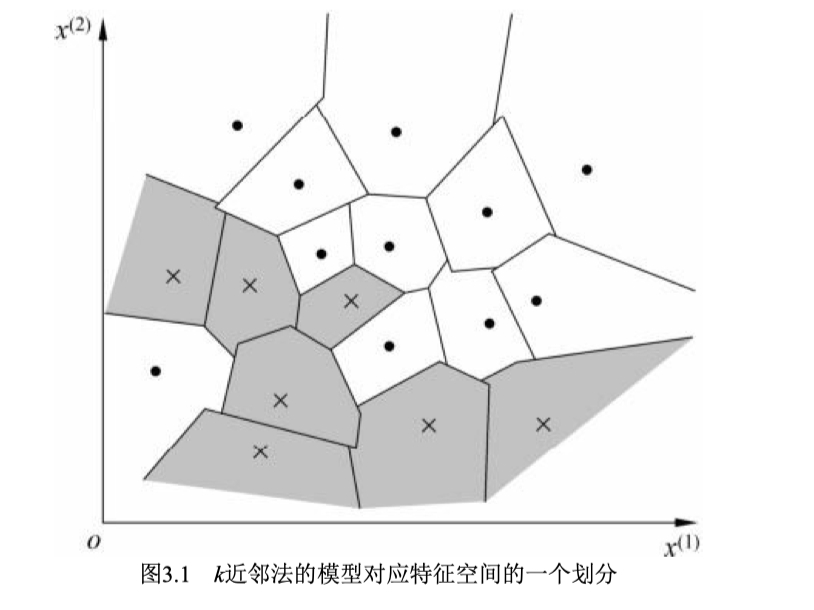
距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映,k近邻模型的特征空间一般是n维实数向量空间$R^n$,使用的距离是欧氏距离,但也可以是其他距离,如更一般的$L_p$距离($L_p$ distance)或Minkowski距离(Minkowski distance)

k值的选择
k值的选择会对k近邻法的结果产生重大影响:
- 如果较小:k值的减小就意味着整体模型变得复杂,容易发生过拟合
- 如果较大:k值的增大就意味着整体的模型变得简单
分类决策规则
k近邻法中的分类决策规则往往是多数表决(majority voting rule),即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类,实际上等价于经验风险最小化
k近邻法的实现:kd树
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索
k近邻法最简单的实现方法是线性扫描(linear scan),这时要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时,这种方法是不可行的
为了提高k近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数,具体方法很多,下面介绍其中的kd树(kd tree)方法
构造kd树
k-d树(k-dimensional树的简称),是一种分割k维数据空间的数据结构,主要应用于多维空间关键数据的搜索(如:范围搜索和最近邻搜索)
k-d树是二叉树,表示对k维空间的一个划分(partition),其中每个结点对应于一 个k维超矩形区域,且该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树

实际做一道例题有助于对算法的理解:
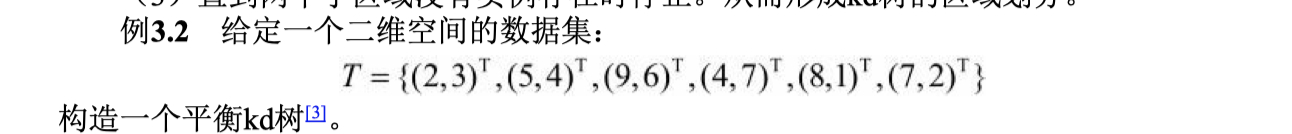
- 首先对数据集排序:(2,3),(4,7),(5,4),(7,2),(8,1),(9,6),其中值为(7,2)
- 根结点生成深度为1的左、右子结点,(2,3),(4,7),(5,4)挂在(7,2)节点的左子树,(8,1),(9,6)挂在(7,2)节点的右子树
- 构建(7,2)节点的左子树,此时切分维度k=2(可以理解为y轴),中值(5,4)作为分割平面,(2,3)挂在其左子树,(4,7)挂在其右子树
- 构建(7,2)节点的右子树,此时切分维度k=2(可以理解为y轴),中值(6,6)作为分割平面
- 无法继续划分,k-d tree构建完成
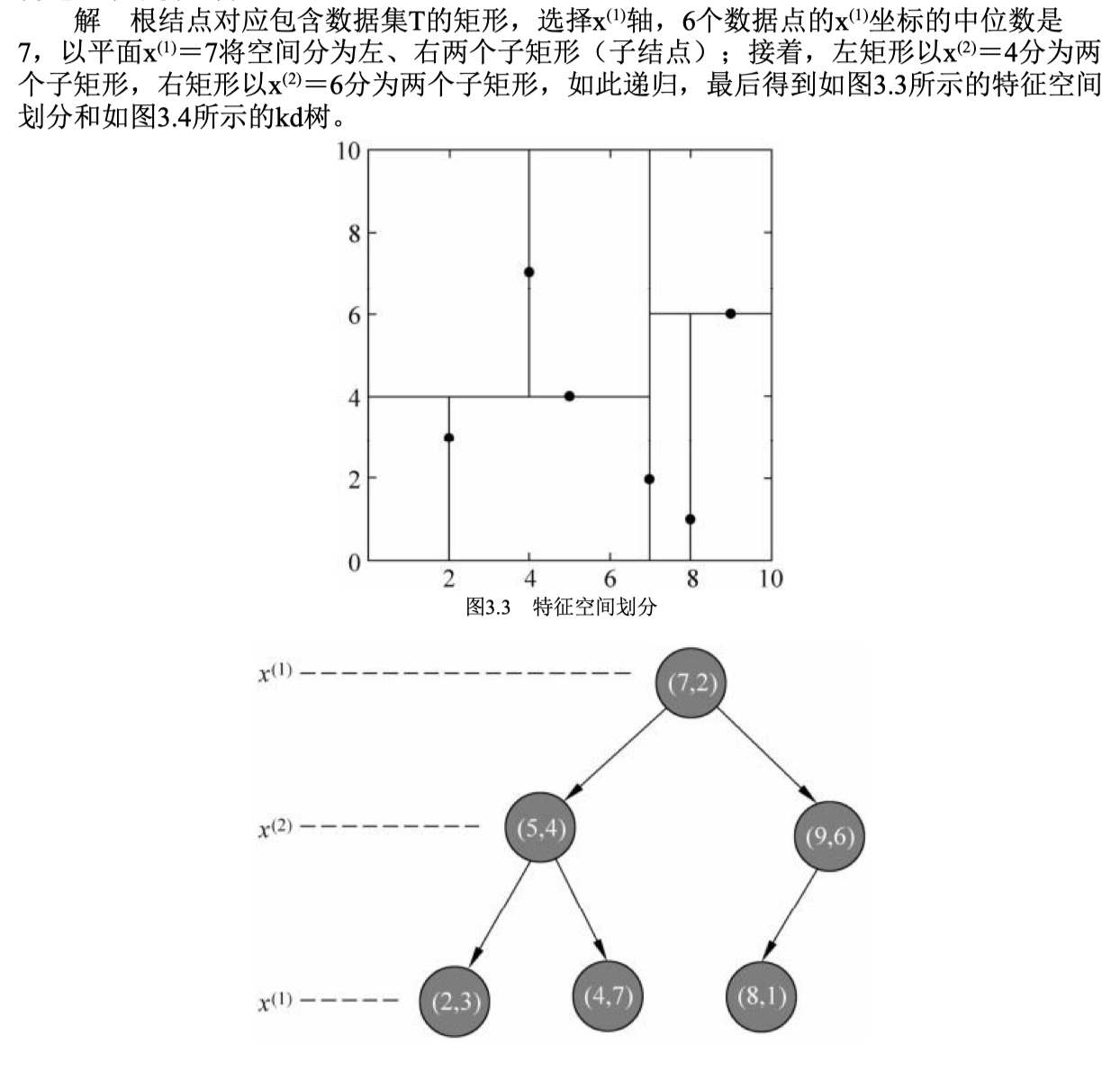
搜索kd树
给定一个目标点,搜索其最近邻,首先找到包含目标点的叶结点;然后从该叶结点出发,依次回退到父结点;不断查找与目标点最邻近的结点,当确定不可能存在更近的结点时终止。这样搜索就被限制在空间的局部区域上,效率大为提高

说明
有助于理解kd树的博客文章:
- 原文作者:howie.hu
- 原文链接:https://www.howie6879.com/post/2018/06_39/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
