如何用Python创建一个简单的神经网络

理解神经网络如何工作的最好方式是自己动手创建一个，这篇文章将会给你演示怎么做到这一点

神经网络(NN)，也称之为人工神经网络(ANN)，它是机器学习领域中学习算法集合中的子集，其核心概念略似生物神经网络的概念。

拥有五年以上经验的德国机器学习专家Andrey Bulezyuk说过：神经网络正在使机器学习发生革命性的巨变，因为他们能够跨越广泛的学科和行业来高效地建模复杂的抽象。

基本上，一个ANN由以下组件构成：

  • 输入层：接受传递数据
  • 隐藏层
  • 输出层
  • 各层之间的权重
  • 每个隐藏层都会有一个精心设计的激活函数，对于此教程，我们将会使用Sigmoid激活函数

神经网络的类型有很多，在这个项目中，我们准备创建一个前馈神经网络，此类型的ANN将会直接从前到后传递数据

训练前馈神经元往往需要反向传播，反向传播为神经网络提供了相应的输入和输出集合，输入数据在被传递到神经元的时候被处理，然后产生一个输出

下面展示了一个简单的神经网络结构图：

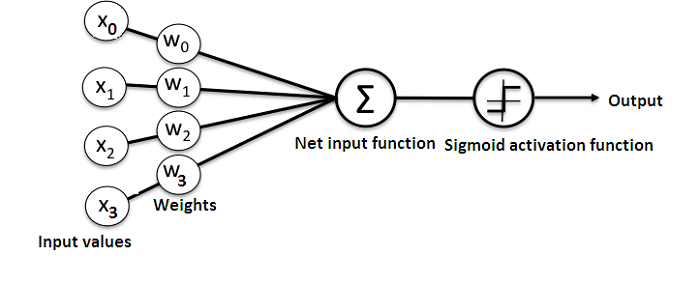
而且，理解神经网络如何工作做好的办法就是去学习从头开始构建一个神经网络(不使用任何第三方库，作者意思应该是不使用任何机器学习库)。

在本文中，我们将演示如何使用Python编程语言创建一个简单的神经网络。

问题

这里用表格列出了我们需要解决的问题：

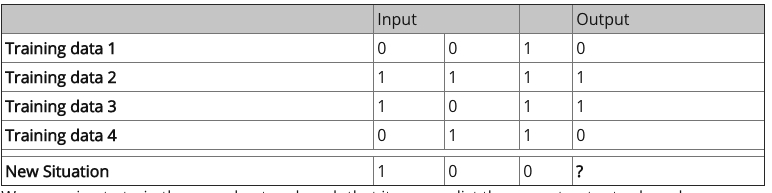
我们将会训练一个特定的神经网络模型，当提供一组新数据的时候，使其能够准确地预测输出值。

如你在表中所见，输出值总是等于输入数据的第一个值，因此我们期望的表中输出(?)值是1。

让我们思考看看能不能使用一些Python代码来给出相同的结果(再继续阅读之前，你可以在文章末尾仔细地阅读此项目的代码)

创建一个神经网络类

我们将在Python中创建一个NeuralNetwork类来训练神经元以提供准确的预测，该类还具有一些其他的辅助函数

尽管我们没有使用任何一个神经网络库用于这个简单的神经网络示例，我们也会导入numpy包来协助计算。

该库带有以下四个重要方法：

  • exp：用于生成自然指数
  • array：用于生成矩阵
  • dot：用于乘法矩阵
  • random：用于生成随机数(注意：我们将对随机数进行播种以确保其有效分布)

应用 Sigmoid 激活函数

该神经网络将使用Sigmoid function作为激活函数，其绘制了一个典型的S形曲线：

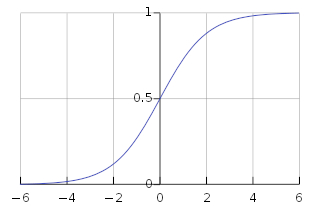
此函数可以将任意值映射到区间0~1之间，它将帮助我们规范化输入值的和权重乘积之和。

随后，我们将创建Sigmoid函数的导数来帮助计算机对权重进行必要的调整。

一个Sigmoid函数的输出可以用来生成它的导数，例如，如果输出变量是X，那么它的导数将是x * (1-x)。

推导过程如下：

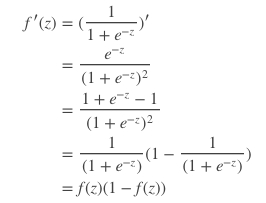
训练模型

在这个阶段我们将教导神经网络进行准确预测，每个输入都有一个权重 - 正面或负面。

这意味着，如果输入包含一个大的正面或者负面的权重数值将会更多地影响输出值

请记住，在最开始阶段我们会对每个权重分配一个随机值

下面是我们在这个神经网络示例问题中使用的训练过程:

  • 从训练集获取输入数据，根据他们的权重进行调整，然后通过计算人工神经网络输出的方法将它们抽取出来
  • 我们计算了反向传播的错误率，在这种情况下，它是神经元预测值和实际期望值之间的差异
  • 根据误差程度，我们利用Error Weighted Derivative formula对权重进行微调
  • 我们对这个过程重复15,000次，在每次迭代中都会同时处理整个训练集

我们使用.T函数将矩阵从水平位置转换到垂直位置，因此数据会被这样排序：

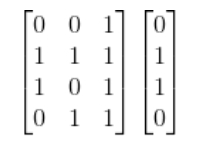
最终，神经元的权重将会被提供的训练集优化，因此，如果神经元被要求去思考一个新的情况，而这个情况和前面的情况是一样的，那么神经元就可以做出准确的预测，这就是反向传播的发生方式。

总结

最终我们初始化了NeuralNetwork类并且运行代码

下面就是整体的项目代码，如何在Python项目中创建神经网络：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

import numpy as np

class NeuralNetwork():
    
    def __init__(self):
        # seeding for random number generation
        np.random.seed(1)
        
        # converting weights to a 3 by 1 matrix with values from -1 to 1 and mean of 0
        self.synaptic_weights = 2 * np.random.random((3, 1)) - 1

    def sigmoid(self, x):
        #applying the sigmoid function
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        #computing derivative to the Sigmoid function
        return x * (1 - x)

    def train(self, training_inputs, training_outputs, training_iterations):
        
        #training the model to make accurate predictions while adjusting weights continually
        for iteration in range(training_iterations):
            #siphon the training data via  the neuron
            output = self.think(training_inputs)

            #computing error rate for back-propagation
            error = training_outputs - output
            
            #performing weight adjustments
            adjustments = np.dot(training_inputs.T, error * self.sigmoid_derivative(output))

            self.synaptic_weights += adjustments

    def think(self, inputs):
        #passing the inputs via the neuron to get output   
        #converting values to floats
        
        inputs = inputs.astype(float)
        output = self.sigmoid(np.dot(inputs, self.synaptic_weights))
        return output


if __name__ == "__main__":

    #initializing the neuron class
    neural_network = NeuralNetwork()

    print("Beginning Randomly Generated Weights: ")
    print(neural_network.synaptic_weights)

    #training data consisting of 4 examples--3 input values and 1 output
    training_inputs = np.array([[0,0,1],
                                [1,1,1],
                                [1,0,1],
                                [0,1,1]])

    training_outputs = np.array([[0,1,1,0]]).T

    #training taking place
    neural_network.train(training_inputs, training_outputs, 15000)

    print("Ending Weights After Training: ")
    print(neural_network.synaptic_weights)

    user_input_one = str(input("User Input One: "))
    user_input_two = str(input("User Input Two: "))
    user_input_three = str(input("User Input Three: "))
    
    print("Considering New Situation: ", user_input_one, user_input_two, user_input_three)
    print("New Output data: ")
    print(neural_network.think(np.array([user_input_one, user_input_two, user_input_three])))
    print("Wow, we did it!")

我们设法创建了一个简单的神经网络。

这个神经网络开始于自己给自己分配了一些随机的权重，此后，它使用训练数据训练自己。

因此，如果出现新情况[1,0,0]，则其值为0.9999584。

你记得我们想要的正确答案是1吗？

那么，这就非常接近了 —— 思考下S形函数的输出值在0到1之间。

当然，我们只使用一个神经网络来执行这个简单的任务，如果我们连接数千个人工神经网络起来会怎样？我们能否100% 地模仿人类大脑的工作方式么？

如果你有任何疑问，请留言

个人简历：Dr. Michael J. Garbade