要想入门以及往下理解深度学习,其中一些概念可能是无法避免地需要你理解一番,比如,备份地址:
- 什么是感知器
- 什么是神经网络
- 张量以及运算
- 微分
- 梯度下降
带着问题出发
在开始之前希望你有一点机器学习方面的知识,解决问题的前提是提出问题,我们提出这样一个问题,对MNIST数据集进行分析,然后在解决问题的过程中一步一步地来捋清楚其中涉及到的概念
MNIST数据集是一份手写字训练集,出自MNIST,相信你对它不会陌生,它是机器学习领域的一个经典数据集,感觉任意一个教程都拿它来说事,不过这也侧面证明了这个数据集的经典,这里简单介绍一下:
- 拥有60,000个示例的训练集,以及10,000个示例的测试集
- 图片都由一个28 ×28 的矩阵表示,每张图片都由一个784 维的向量表示
- 图片分为10类, 分别对应从0~9,共10个阿拉伯数字
压缩包内容如下:
- train-images-idx3-ubyte.gz: training set images (9912422 bytes)
- train-labels-idx1-ubyte.gz: training set labels (28881 bytes)
- t10k-images-idx3-ubyte.gz: test set images (1648877 bytes)
- t10k-labels-idx1-ubyte.gz: test set labels (4542 bytes)
上图:

图片生成代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = instances
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(9,9))
plot_digits(train_images[:100], images_per_row=10)
plt.show()
|
不过你不用急着尝试,接下来我们可以一步一步慢慢来分析手写字训练集
看这一行代码:
1
|
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
|
MNIST数据集通过keras.datasets加载,其中train_images和train_labels构成了训练集,另外两个则是测试集:
- train_images.shape: (60000, 28, 28)
- train_labels.shape: (60000,)
我们要做的事情很简单,将训练集丢到神经网络里面去,训练后生成了我们期望的神经网络模型,然后模型再对测试集进行预测,我们只需要判断预测的数字是不是正确的即可
在用代码构建一个神经网络之前,我先简单介绍一下到底什么是神经网络,让我们从感知器开始
感知器
感知器是Frank Rosenblatt提出的一个由两层神经元组成的人工神经网络,它的出现在当时可是引起了轰动,因为感知器是首个可以学习的神经网络
感知器的工作方式如下所示:

左侧三个变量分别表示三个不同的二进制输入,output则是一个二进制输出,对于多种输入,可能有的输入成立有的不成立,在这么多输入的影响下,该如何判断输出output呢?Rosenblatt引入了权重来表示相应输入的重要性

此时,output可以表示为:

上面右侧的式子是一个阶跃函数,就是和Sigmoid、Relu一样作用的激活函数,然后我们就可以自己实现一个感知器:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
import numpy as np
class Perceptron:
"""
代码实现 Frank Rosenblatt 提出的感知器的与非门,加深对感知器的理解
blog: https://www.howie6879.cn/post/33/
"""
def __init__(self, act_func, input_nums=2):
"""
实例化一些基本参数
:param act_func: 激活函数
"""
# 激活函数
self.act_func = act_func
# 权重 已经确定只会有两个二进制输入
self.w = np.zeros(input_nums)
# 偏置项
self.b = 0.0
def fit(self, input_vectors, labels, learn_nums=10, rate=0.1):
"""
训练出合适的 w 和 b
:param input_vectors: 样本训练数据集
:param labels: 标记值
:param learn_nums: 学习多少次
:param rate: 学习率
"""
for i in range(learn_nums):
for index, input_vector in enumerate(input_vectors):
label = labels[index]
output = self.predict(input_vector)
delta = label - output
self.w += input_vector * rate * delta
self.b += rate * delta
print("此时感知器权重为{0},偏置项为{1}".format(self.w, self.b))
return self
def predict(self, input_vector):
if isinstance(input_vector, list):
input_vector = np.array(input_vector)
return self.act_func(sum(self.w * input_vector) + self.b)
def f(z):
"""
激活函数
:param z: (w1*x1+w2*x2+...+wj*xj) + b
:return: 1 or 0
"""
return 1 if z > 0 else 0
def get_and_gate_training_data():
'''
AND 训练数据集
'''
input_vectors = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
labels = np.array([1, 0, 0, 0])
return input_vectors, labels
if __name__ == '__main__':
"""
输出如下:
此时感知器权重为[ 0.1 0.2],偏置项为-0.2 与门
1 and 1 = 1
1 and 0 = 0
0 and 1 = 0
0 and 0 = 0
"""
# 获取样本数据
and_input_vectors, and_labels = get_and_gate_training_data()
# 实例化感知器模型
p = Perceptron(f)
# 开始学习 AND
p_and = p.fit(and_input_vectors, and_labels)
# 开始预测 AND
print('1 and 1 = %d' % p_and.predict([1, 1]))
print('1 and 0 = %d' % p_and.predict([1, 0]))
print('0 and 1 = %d' % p_and.predict([0, 1]))
print('0 and 0 = %d' % p_and.predict([0, 0]))
|
S型神经元
神经元和感知器本质上是一样的,他们的区别在于激活函数不同,比如跃迁函数改为Sigmoid函数
神经网络可以通过样本的学习来调整人工神经元的权重和偏置,从而使输出的结果更加准确,那么怎样给⼀个神经⽹络设计这样的算法呢?

以数字识别为例,假设⽹络错误地把⼀个9的图像分类为8,我们可以让权重和偏置做些⼩的改动,从而达到我们需要的结果9,这就是学习。对于感知器,我们知道,其返还的结果不是0就是1,很可能出现这样一个情况,我们好不容易将一个目标,比如把9的图像分类为8调整回原来正确的分类,可此时的阈值和偏置会造成其他样本的判断失误,这样的调整不是一个好的方案
所以,我们需要S型神经元,因为S型神经元返回的是[0,1]之间的任何实数,这样的话权重和偏置的微⼩改动只会引起输出的微⼩变化,此时的output可以表示为σ(w⋅x+b),而σ就是S型函数,S型函数中S指的是Sigmoid函数,定义如下:

神经网络
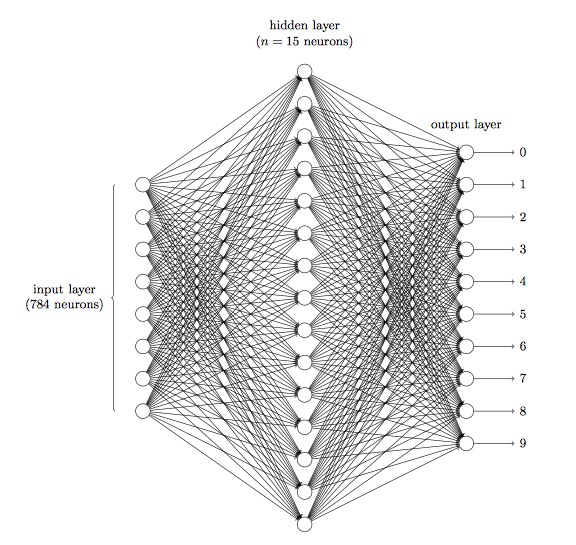
神经网络其实就是按照一定规则连接起来的多个神经元,一个神经网络由以下组件构成:
- 输入层:接受传递数据,这里应该是 784 个神经元
- 隐藏层:发掘出特征
- 各层之间的权重:自动学习出来
- 每个隐藏层都会有一个精心设计的激活函数,比如Sigmoid、Relu激活函数
- 输出层,10个输出
- 上⼀层的输出作为下⼀层的输⼊,信息总是向前传播,从不反向回馈:前馈神经网络
- 有回路,其中反馈环路是可⾏的:递归神经网络
从输入层传入手写字训练集,然后通过隐藏层向前传递训练集数据,最后输出层会输出10个概率值,总和为1。现在,我们可以看看Keras代码:
第一步,对数据进行预处理,我们知道,原本数据形状是(60000, 28, 28),取值区间为[0, 255],现在改为[0, 1]:
1
2
3
4
5
|
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
|
然后对标签进行分类编码:
1
2
3
4
|
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
|
第二步,编写模型:
1
2
3
4
5
6
7
8
9
|
from keras import models
from keras import layers
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax')
network.compile(optimizer='rmsprop',loss='categorical_crossentropy', metrics=['accuracy'])
network.fit(train_images, train_labels, epochs=5, batch_size=128)
|
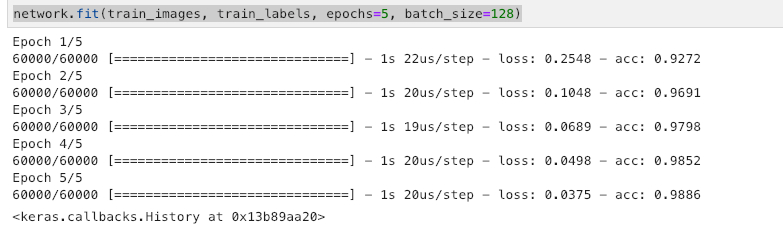
一个隐藏层,激活函数选用relu,输出层使用softmax返回一个由10个概率值(总和为 1)组成的数组
训练过程中显示了两个数字:一个是网络在训练数据上的损失loss,另一个是网络在 训练数据上的精度acc

很简单,我们构建和训练一个神经网络,就这么几行代码,之所以写的这么剪短,是因为keras接接口封装地比较好用,但是里面的理论知识我们还是需要好好研究下
神经网络的数据表示
TensorFlow里面的Tensor是张量的意思,上面例子里面存储在多维Numpy数组中的数据就是张量:张量是数据容器,矩阵就是二维张量,张量是矩阵向任意维度的推广,张量的维度称为轴
标量
包含一个数字的张量叫做标量(0D张量),如下:
1
2
3
|
x = np.array(12)
print(x, x.ndim)
# 12, 0
|
张量轴的个数也叫做阶(rank)
向量
数字组成的数组叫做向量(1D张量),如下:
1
2
3
|
x = np.array([12, 3, 6, 14, 7])
print(x, x.ndim)
# [12 3 6 14 7] 1
|
矩阵
向量组成的数组叫做矩阵(2D张量),如下:
1
2
3
4
5
|
x = np.array([[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]])
print(x, x.ndim)
# [[ 5 78 2 34 0]
# [ 6 79 3 35 1]
# [ 7 80 4 36 2]] 2
|
3D张量与更高维张量
将多个矩阵组合成一个新的数组就是一个3D张量,如下:
1
2
3
4
5
6
7
8
9
10
|
x = np.array([[[5, 78, 2, 34, 0], [6, 79, 3, 35, 1]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1]]])
print(x, x.ndim)
# (array([[[ 5, 78, 2, 34, 0],
# [ 6, 79, 3, 35, 1]],
#
# [[ 5, 78, 2, 34, 0],
# [ 6, 79, 3, 35, 1]],
#
# [[ 5, 78, 2, 34, 0],
# [ 6, 79, 3, 35, 1]]]), 3)
|
将多个3D张量组合成一个数组,可以创建一个4D张量
关键属性
张量是由以下三个关键属性来定义:
- 轴的个数:3D张量三个轴,矩阵两个轴
- 形状:是一个整数元祖,比如前面矩阵为(3, 5),向量(5,),3D张量为(3, 2, 5)
- 数据类型
在Numpy中操作张量
以前面加载的train_images为:
1
|
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
|
比如进行切片选择10~100个数字:
1
2
|
train_images[10:100].shape
# (90, 28, 28)
|
数据批量的概念
深度学习模型会将数据集随机分割成小批量进行处理,比如:
1
2
3
|
batch = train_images[:128]
batch.shape
# (128, 28, 28)
|
现实世界的数据张量
下面将介绍下现实世界中数据的形状:
- 向量数据:2D张量,(samples, features)
- 时间序列数据或者序列数据:3D张量,(samples, timesteps, features)
- 图像:4D张量,(samples, height, width, channels) 或 (samples, channels, height, width)
- 视频:5D张量,(samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)
张量运算
类似于计算机程序的计算可以转化为二进制计算,深度学习计算可以转化为数值数据张量上的一些张量运算(tensor operation)
上面模型的隐藏层代码如下:
1
|
keras.layers.Dense(512, activation='relu')
|
这一层可以理解为一个函数,输入一个2D张量,输出一个2D张量,就如同上面感知机那一节最后输出的计算函数:
1
|
output = relu(dot(W, input) + b)
|
逐元素计算
Relu 和加法运算都是逐元素的运算,比如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
# 输入示例
input_x = np.array([[2], [3], [1]])
# 权重
W = np.array([[5, 6, 1], [7, 8, 1]])
# 计算输出 z
z = np.dot(W, input_x)
# 实现激活函数
def naive_relu(x):
assert len(x.shape) == 2
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] = max(x[i, j], 0)
return x
# 激活函数对应的输出
output = naive_relu(z)
output
|
广播
张量运算那节中,有这样一段代码:
1
|
output = relu(dot(W, input) + b)
|
dot(W, input)是2D张量,b是向量,两个形状不同的张量相加,会发生什么?
如果没有歧义的话,较小的张量会被广播,用来匹配较大张量的形状:
1
2
3
4
5
6
7
8
|
input_x = np.array([[1], [3]])
# 权重
W = np.array([[5, 6], [7, 8]])
b = np.array([1])
# 计算输出 z
z = np.dot(W, input_x) + b
# array([[24],
# [32]])
|
张量点积
点积运算,也叫张量积,如:
1
2
3
4
5
6
7
|
import numpy as np
# 输入示例
input_x = np.array([[2], [3], [1]])
# 权重
W = np.array([[5, 6, 1], [7, 8, 1]])
np.dot(W, input_x)
|
两个向量之间的点积是一个标量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z
x = np.array([1,2])
y = np.array([1,2])
naive_vector_dot(x, y)
# 5.0
|
矩阵和向量点积后是一个向量:
1
2
|
np.dot(W, [1, 2, 3])
# array([20, 26])
|
张量变形
前面对数据进行预处理的时候:
1
2
|
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
|
上面的例子将输入数据的shape变成了(60000, 784),张量变形指的就是改变张量的行和列,得到想要的形状,前后数据集个数不变,经常遇到一个特殊的张量变形是转置(transposition),如下:
1
2
3
4
|
x = np.zeros((300, 20))
x = np.transpose(x)
x.shape
# (20, 300)
|
梯度优化
针对每个输入,神经网络都会通过下面的函数对输入数据进行变换:
1
|
output = relu(dot(W, input_x) + b)
|
其中:
- relu:激活函数
- W:是一个张量,表示权重,第一步可以取较小的随机值进行随机初始化
- b:是一个张量,表示偏置
现在我们需要一个算法来让我们找到权重和偏置,从而使得y=y(x)可以拟合样本输入的x
再回到感知器
感知器学习的过程就是其中权重和偏置不断调优更新的过程,其中的偏置可以理解成输入为1的权重值,那么权重是怎么更新的呢?
首先,介绍一个概念,损失函数,引用李航老师统计学习方法书中的一个解释:
监督学习问题是在假设空间中选取模型f作为决策函数,对于给定的输入X,由f(X)给出相应的输出Y,这个输出的预测值f(X)与真实值Y可能一致也可能不一致,用一个损失函数(loss function)或代价函数(cost function)来度量预测错误的程度,损失函数是f(X)和Y的非负实值函数,记作L(Y,f(X))
其中模型f(X)关于训练数据集的平均损失,我们称之为:经验风险(empirical risk),上述的权重调整,就是在不断地让经验风险最小,求出最好的模型f(X),我们暂时不考虑正则化,此时我们经验风险的最优化的目标函数就是:

求解出此目标函数最小时对应的权重值,就是我们感知器里面对应的权重值,在推导之前,我们还得明白两个概念:
什么是导数
假设有一个连续的光滑函数f(x) = y,什么是函数连续性?指的是x的微小变化只能导致y的微小变化。
假设f(x)上的两点a,b足够接近,那么a,b可以近似为一个线性函数,此时他们斜率为k,那么可以说斜率k是f在b点的导数
总之,导数描述了改变x后f(x)会如何变化,如果你希望减小f(x)的值,只需要将x沿着导数的反方向移动一小步即可,反之亦然
什么是梯度
梯度是张量运算的导数,是导数这一概念向多元函数导数的推广,它指向函数值上升最快的方向,函数值下降最快的方向自然就是梯度的反方向
随机梯度下降
推导过程如下:

感知器代码里面的这段:
1
|
self.w += input_vector * rate * delta
|
就对应上面式子里面推导出来的规则
总结
再来看看全部的手写字识别模型代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
from keras import models
from keras import layers
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))
network.compile(optimizer='rmsprop',loss='categorical_crossentropy', metrics=['accuracy'])
network.fit(train_images, train_labels, epochs=5, batch_size=128)
test_loss, test_acc = network.evaluate(test_images, test_labels)
print('test_acc:', test_acc)
|
- 输入数据保存在
float32格式的Numpy张量中,形状分别是(60000, 784)和(10000, 784)
- 神经网络结构为:1个输入层、一个隐藏层、一个输出层
- categorical_crossentropy是针对分类模型的损失函数
- 每批128个样本,共迭代5次,一共更新(469 * 5) = 2345次
说明
对本文有影响的书籍文章如下,感谢他们的付出:













