前面一章，我们通过了梯度下降算法实现目标函数的最小化，从而学习了该神经网络的权重和偏置，但是有一个问题并没有考虑到，那就是如何计算代价函数的梯度，本章的重点就是介绍计算这些梯度的快速算法——反向传播算法，首先先介绍一下上图中以及下面文章中会出现的一些数学符号：

  • $L$ : 表示网络层数
  • $b_j^l$ : 表示第$l$层的第$j$个神经元的偏置
  • $a_j^l$ : 表示第$l$层的第$j$个神经元的激活值
  • $w_{j k}^{l}$ : 表示从$l-1$层的第$k$个神经元到第$l$层的第$j$个神经元的连接上的权重
  • $w^l$ : 权重矩阵，其中元素表示$l-1$层连接到$l$层神经元的权重
  • $b^l$ : 第$l$层神经元的偏置向量
  • $z^l$ : 第$l$层神经元的带权输入向量
  • $a^l$ : 第$l$层每个神经元激活值构成的向量
  • $\delta_{j}^{l}$ : 第$l$层第$j$个神经元的误差

本篇文章是公式重灾区，但是涉及的知识并不高级，这也说明一个道理：

很多看似显而易见的想法只有在事后才变得显而易见。

热⾝：神经⽹络中使⽤矩阵快速计算输出的⽅法

通过第一章，我们已经知道每个神经元的激活值的计算方法，根据上面的公式，我们可以得出$a_j^l$的表达方式：

$$ a_{j}^{l}=\sigma\left(\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}\right) $$

举个例子：$a_3^2$表示第二层的第三个神经元的激活值，那么该输出值怎么同上一层的输出值以及权重关联起来的呢，根据激活值的计算公式，我们可以得出：

$$ \begin{aligned} a_3^2 &= \sigma(w_{3 1}^{2} a_1^1 + w_{3 2}^{2} a_2^1+ w_{3 3}^{2} a_3^1 + b_3^2 ) \ &= \sigma\left(\sum_{k=1}^3 w_{3 k}^2 a_{k}^1 + b_3^2 \right) \end{aligned} $$

可以看到例子中的结果满足表达式，接下来，让我们将表达式改成向量形式：

$$ \begin{aligned} a^{l} &= \sigma\left(w^{l} a^{l-1}+b^{l}\right) \ &= \sigma\left(z^l \right) \end{aligned} $$

这个式子是正确的么，我们实际根据第一层到第二层的计算来看看：

首先定义第一层的激活函数输出值向量$a^1$:

$$ {a^1} = \left[ \begin{array}{c}{a_1^1} \ {a_2^1} \ {a_3^1} \end{array}\right] $$

然后是第一层神经元连接到第二层神经元的权重矩阵：

$$ {w^2} = \left[ \begin{array}{c}{w_{1 1}^2,w_{1 2}^2,w_{1 3}^2} \ {w_{2 1}^2,w_{2 2}^2,w_{2 3}^2} \ {w_{3 1}^2,w_{3 2}^2,w_{3 3}^2} \ {w_{4 1}^2,w_{4 2}^2,w_{4 3}^2} \end{array}\right] $$

同理，第二层神经元的偏置向量：

$$ {b^2} = \left[ \begin{array}{c}{b_1^2} \ {b_2^2} \ {b_3^2} \ {b_4^2} \end{array}\right] $$

我们的目标是求得第二层神经元激活值构成的向量$a^2$:

$$ {a^2} = \left[ \begin{array}{c}{a_1^2} \ {a_2^2} \ {a_3^2} \ {a_4^2} \end{array}\right] $$

激活值计算如下：

$$ \begin{aligned} a^2 &= \sigma(w^2a^1 + b^2) \&= \sigma\left(\left[ \begin{array}{c}{w_{1 1}^2,w_{1 2}^2,w_{1 3}^2} \ {w_{2 1}^2,w_{2 2}^2,w_{2 3}^2} \ {w_{3 1}^2,w_{3 2}^2,w_{3 3}^2} \ {w_{4 1}^2,w_{4 2}^2,w_{4 3}^2} \end{array}\right] \left[ \begin{array}{c}{a_1^1} \ {a_2^1} \ {a_3^1} \end{array}\right] + \left[ \begin{array}{c}{b_1^2} \ {b_2^2} \ {b_3^2} \ {b_4^2} \end{array}\right]\right) \end{aligned} $$

$$ {a^2} = \left[ \begin{array}{c}{a_1^2} \ {a_2^2} \ {a_3^2} \ {a_4^2} \end{array}\right]=\sigma\left(\left[ \begin{array}{c}{w_{1 1}^2 a_1^1+w_{1 2}^2 a_2^1+w_{1 3}^2 a_3^1}+b_1^2 \ {w_{2 1}^2 a_1^1+w_{2 2}^2 a_2^1+w_{2 3}^2 a_3^1}+b_2^2 \ {w_{3 1}^2 a_1^1+w_{3 2}^2 a_2^1+w_{3 3}^2 a_3^1}+b_3^2 \ {w_{4 1}^2 a_1^1+w_{4 2}^2 a_2^1+w_{4 3}^2 a_3^1}+b_4^2 \end{array}\right]\right) $$

可以看到$a_3^2$的值和前面第一次举例子算出来的值一致。

关于代价函数的两个假设

我们以均方误差得出的代价函数如下：

$$ C=\frac{1}{2 n} \sum_{x}\left|y(x)-a^{L}(x)\right|^{2} $$

公式说明：

  • $y(x)$是目标输出
  • $a^{L}(x)$是当输入是$x$时候网络输出的激活值向量

好了，为了应⽤反向传播，我们需要对代价函数 $C$ 做出什么样的前提假设呢？

第一：代价函数可以被写成⼀个在每个训练样本 $x$ 上的代价函数 $C_x$ 的均值:

$$ C=\frac{1}{n} \sum_{x} C_{x} $$

第⼆：代价可以写成神经⽹络输出的函数：

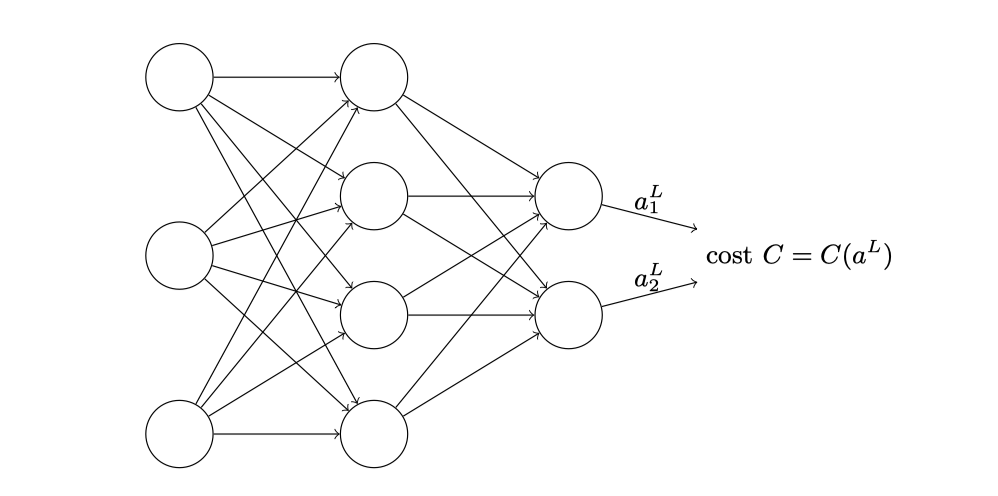
为对于⼀个单独的训练样本 $x$ 其⼆次代价函数可以写作：

$$ C=\frac{1}{2}\left|y-a^{L}\right|^{2}=\frac{1}{2} \sum_{j}\left(y_{j}-a_{j}^{L}\right)^{2} $$

反向传播的四个基本方程

反向传播其实是对权重和偏置变化影响代价函数过程的理解，最终极的含义其实就是计算偏导数 $\partial C / \partial w_{j k}^{l}$ 和 $\partial C / \partial b_{j}^{l}$。

为了计算这些值，我们引入一个中间量$\delta_{j}^{l}$ ，其表示的是第$l$层第$j$个神经元的误差，其中$\delta^l$表示第$l$层的误差向量，对于这个误差，我们应该怎样表示呢：

$$ \delta_{j}^{l} \equiv \frac{\partial C}{\partial z_{j}^{l}} $$

接下来要做的就是将这些误差和 $\partial C / \partial w_{j k}^{l}$ 和 $\partial C / \partial b_{j}^{l}$ 联系起来，解决方案就是反向传播基于四个基本⽅程：

输出层误差的⽅程

输出层误差的⽅程，$\delta^L$ ： 每个元素定义如下：

$$ \delta_{j}^{L}=\frac{\partial C}{\partial a_{j}^{L}} \sigma^{\prime}\left(z_{j}^{L}\right) $$

矩阵形式重写⽅程：

$$ \delta^{L}=\nabla_{a} C \odot \sigma^{\prime}\left(z^{L}\right) $$

其中$\nabla_{a}$就是梯度向量，其元素就是偏导数$\partial C / \partial a_{j}^{L}$的所有元素，以上述二次代价函数为例：

$$ C_{x}=\frac{1}{2}\left|y-a^{L}\right|^{2} $$

可以得出：

$$ \nabla_{a} C=\left(a^{L}-y\right) $$

因此方程的矩阵形式可以改成：

$$ \delta^{L}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right) $$

推导过程如下：

使用下一层的误差表示当前层的误差

$$ \delta^{l}=\left(\left(w^{l+1}\right)^{T} \delta^{l+1}\right) \odot \sigma^{\prime}\left(z^{l}\right) $$

推导过程如下：

代价函数关于⽹络中任意偏置的改变率

$$ \frac{\partial C}{\partial b_{j}^{l}}=\delta_{j}^{l} $$

推导过程如下：

代价函数关于任何⼀个权重的改变率

$$ \frac{\partial C}{\partial w_{j k}^{l}}=a_{k}^{l-1} \delta_{j}^{l} $$

推导过程如下：

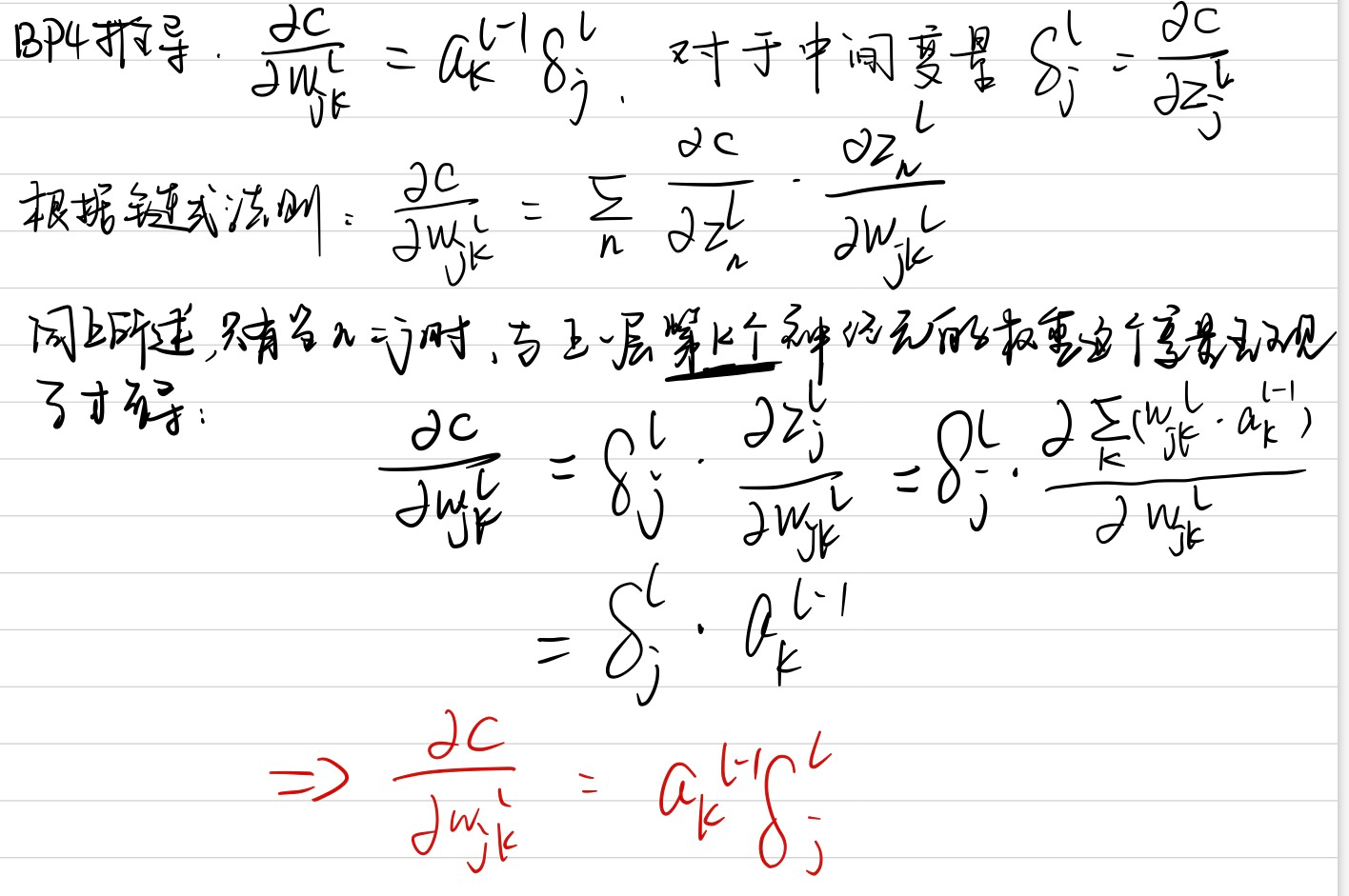
反向传播的四个基本公式，靠着一个链式法则，就全都推下来了，没有什么难度

反向传播算法

反向传播算法给出了一种计算代价函数梯度的方法，算法描述如下：

  • 输入特征x：为输⼊层设置对应的激活值$a^1$
  • 前向传播：对每个$$l=2,3,…,L$$计算相应的$$z^l$$和$$a^l$$
    • $$z^l=w^{l} a^{l-1}+b^{l}$$
    • $$a^l=\sigma(z^l)$$
  • 输出层误差：$$\delta^{L}=\nabla_{a} C \odot \sigma^{\prime}\left(z^{L}\right)$$
  • 反向误差传播：对每个$$l=L-1,L-2,…,2$$，计算$$\delta^{l}=\left(\left(w^{l+1}\right)^{T} \delta^{l+1}\right) \odot \sigma^{\prime}\left(z^{l}\right)$$
  • 输出：代价函数的梯度由$$\frac{\partial C}{\partial w_{j k}^{l}}=a_{k}^{l-1} \delta_{j}^{l}$$和$$\frac{\partial C}{\partial b_{j}^{l}}=\delta_{j}^{l}$$得出

反向传播：全局观

假设我们已经对⼀些⽹络中的 $w_{j k}^l$ 做⼀点⼩⼩的变动 $$\Delta w_{j k}^{l}$$

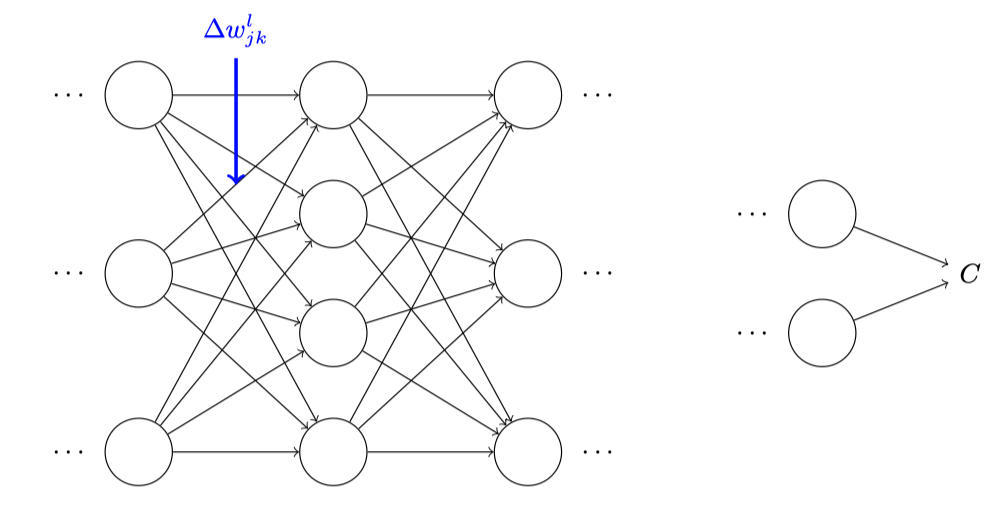
显然，这样会造成输出激活值的改变：

然后，会让下一层所有的激活值产生改变：

接着，这些改变都将影响到⼀个个下⼀层，到达输出层，最终影响代价函数：

根据求导的思想，我们可以得出下面公式：

$$ \Delta C \approx \frac{\partial C}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

我们知道，$$\Delta w_{j k}^{l}$$造成了第$$l$$层的第$$j$$神经元的激活值的变化$$\Delta a_{j}^{l}$$，这个变化由下⾯的公式给出：

$$ \Delta a_{j}^{l} \approx \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

$$\Delta a_{j}^{l}$$的变化会造成下一层所有神经元激活值的变化，我们聚焦到其中⼀个激活值上看看影响的情况，不防设$$a_q^{l+1}$$：

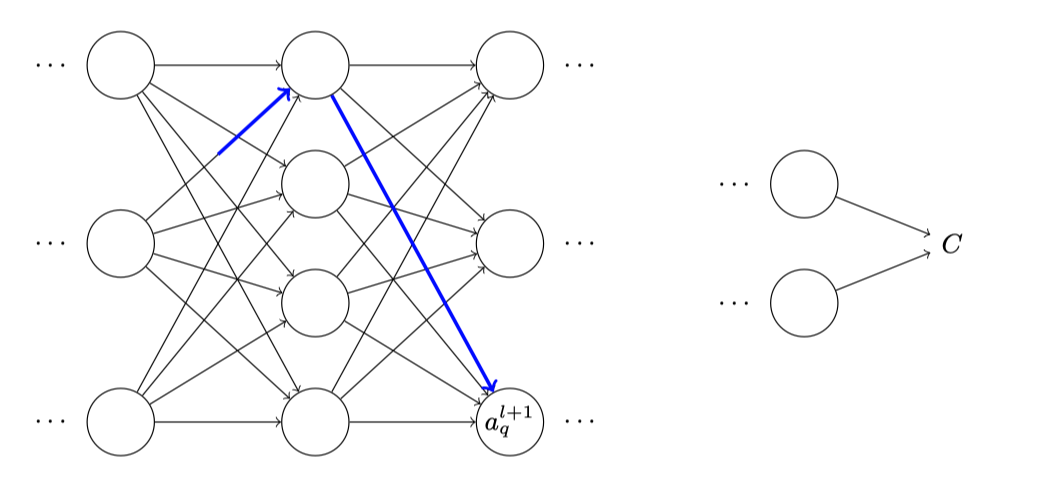
实际上，这会导致下⾯的变化：

$$ \Delta a_{q}^{l+1} \approx \frac{\partial a_{q}^{l+1}}{\partial a_{j}^{l}} \Delta a_{j}^{l} $$

我们已经知道$$\Delta a_{j}^{l} \approx \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \Delta w_{j k}^{l}$$，我们可以得到：

$$ \Delta a_{q}^{l+1} \approx \frac{\partial a_{q}^{l+1}}{\partial a_{j}^{l}} \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

就这样一直传播下去，最终将所有的影响汇聚到输出层代价的变化，假设$$a_{j}^{l}, a_{q}^{l+1}, \ldots, a_{n}^{L-1}, a_{m}^{L}$$，那么结果的表达式就是：

$$ \Delta C \approx \frac{\partial C}{\partial a_{m}^{L}} \frac{\partial a_{m}^{L}}{\partial a_{n}^{L-1}} \frac{\partial a_{n}^{L-1}}{\partial a_{p}^{L-2}} \ldots \frac{\partial a_{q}^{l+1}}{\partial a_{j}^{l}} \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

影响输出层代价的权重值有很多，所以我们需要进行求和：

$$ \Delta C \approx \sum_{m n p_{\ldots q}} \frac{\partial C}{\partial a_{m}^{L}} \frac{\partial a_{m}^{L}}{\partial a_{n}^{L-1}} \frac{\partial a_{n}^{L-1}}{\partial a_{p}^{L-2}} \ldots \frac{\partial a_{q}^{l+1}}{\partial a_{j}^{l}} \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

因为：

$$ \Delta C \approx \frac{\partial C}{\partial w_{j k}^{l}} \Delta w_{j k}^{l} $$

带入上面式子，得出：

$$ \begin{aligned} \frac{\partial C}{\partial w_{j k}^{l}}&=\sum_{m n p \ldots q} \frac{\partial C}{\partial a_{m}^{L}} \frac{\partial a_{m}^{L}}{\partial a_{n}^{L-1}} \frac{\partial a_{n}^{L-1}}{\partial a_{p}^{L-2}} \cdots \frac{\partial a_{q}^{l+1}}{\partial a_{j}^{l}} \frac{\partial a_{j}^{l}}{\partial w_{j k}^{l}} \&=a_{k}^{l-1} \delta_{j}^{l} \end{aligned} $$

想起一句歌词，又回到最初的起点，我们竟然就是在做反向传播，神奇。

参考

搞定收工，有兴趣欢迎关注我的公众号：